Gaurav Verma

Visualizing Exploratory Nature of Individuals

Physicists often fuse the three dimensions of space and the one dimension of time to construct a four-dimensional spacetime continuum. If you've read A Brief History of Time by Stephen Hawking, the following image might jog your memory.

If you're interested in reading more about this particular diagram, you may start on Wikipedia. I, however, will borrow this image from Physics, and use it to visualize exploratory nature of individuals. It's fairly simple stuff; but it intrigues me.

Consider the following image -- two cones meeting at a single point. I will, for convenience, refer to the upper (inverted) cone as the 'future' cone while referring to the one at bottom as the 'past' cone. The point where the two cones meet is present -- it's you in this moment reading this article. And there's going to be only one moment like this in the entire spacetime continuum. Ever.

Moving into the future -- along t⁺, from the current moment we are in (i.e., t = t_c), we make a series of concious and unconcious choices. The choices that we make play a crucial role in determining the path we will follow while entering the future cone. It could be a zigzag one -- like the one in red that the following image shows -- or a straight one (imagine travelling along the height of the cone that runs through t = t_c). There's just one rule: you can't go back in time.

Imagine all the possible places you can end up in, two years down the line. That hypothetical space which encompasses all those possibilities, is represented by the grey circle at t = t_c + 2 years in the above figure. It's worth noting that, under current considerations, all points in that hypothetical space are treated as equal in all wordly senses -- no point is better than the other.

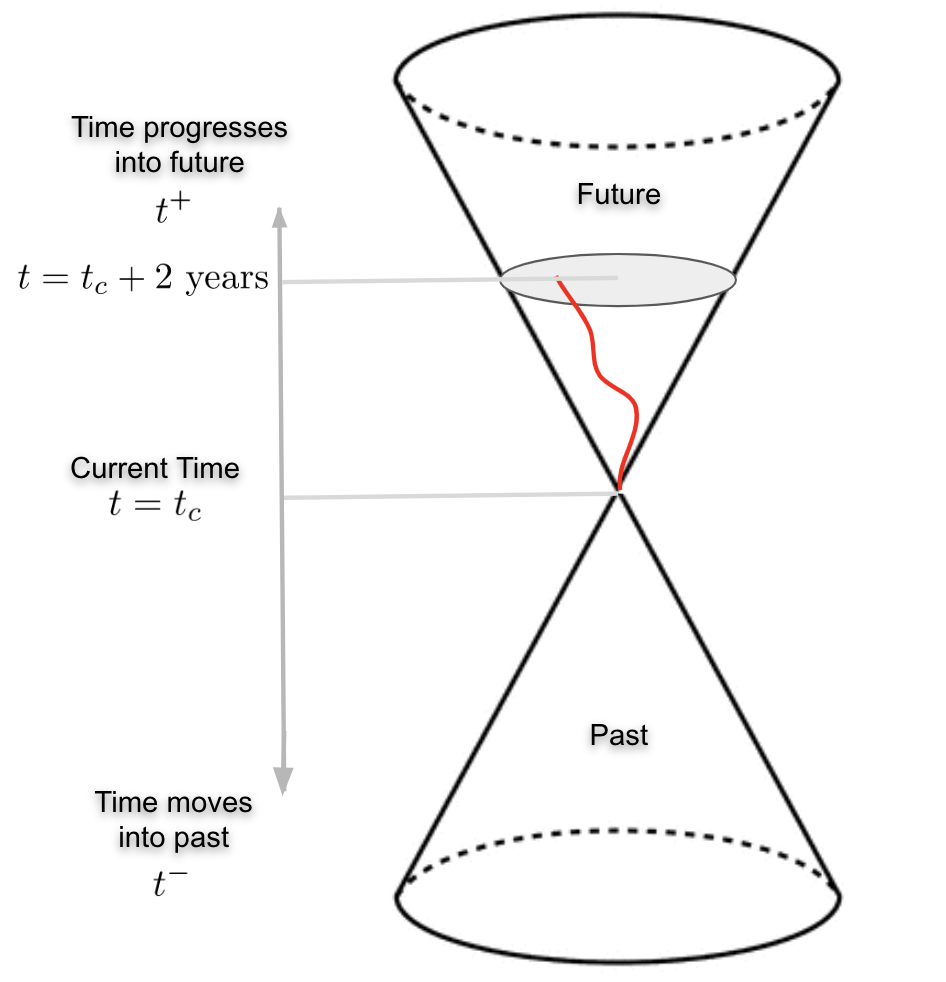
Looking behind, it was our choices that determined the trajectory we followed while getting from t = t_c to t = t_c + 2 years. Those choices are a function of our exploration tendencies. One can argue that our choices are not really ours, and there are other social factors that influcene an individual's exploration tendencies. I agree.
My usage of the phrase 'exploration tendencies' includes those things.

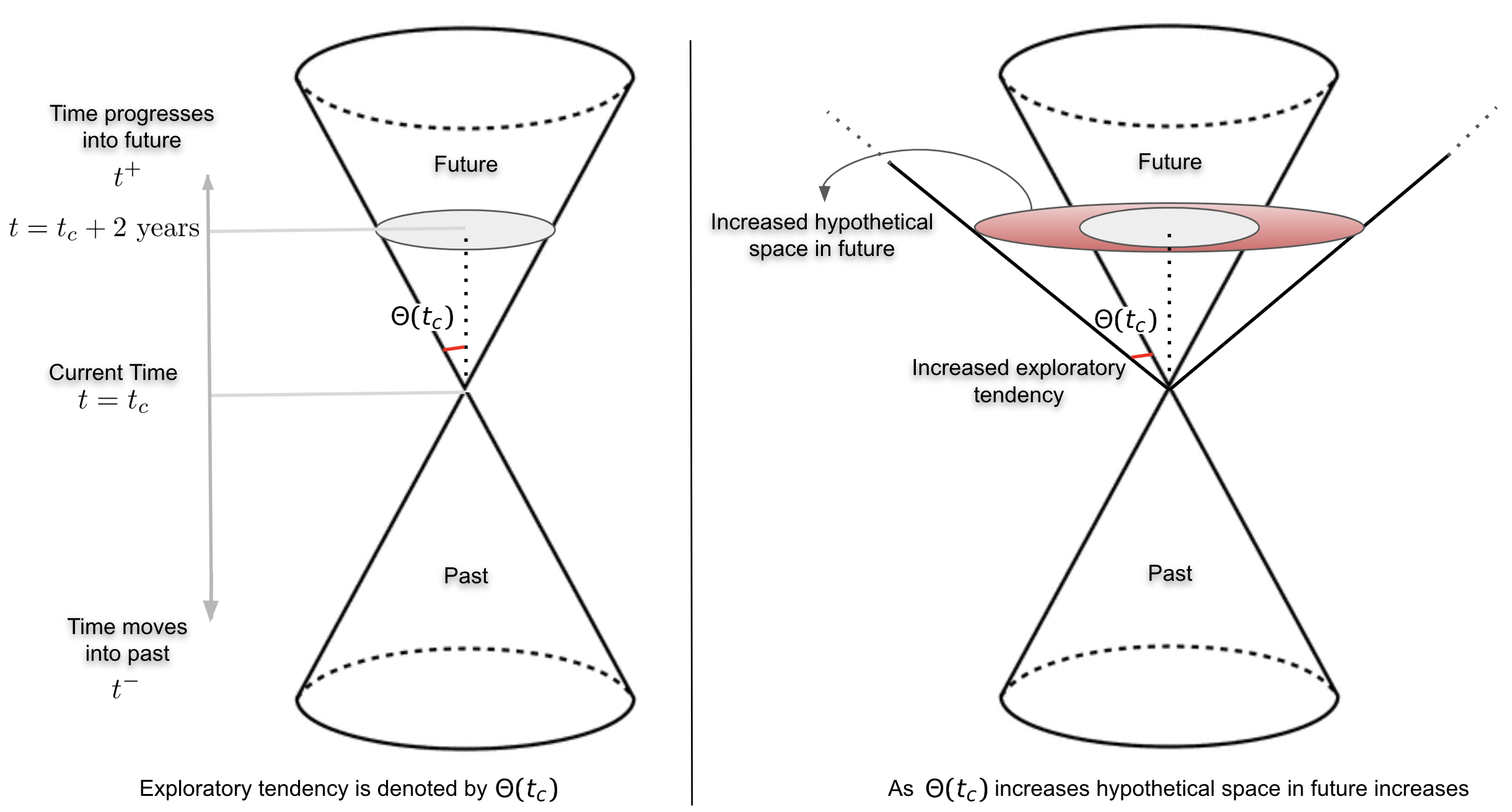
At any given time t = t_c, an individual's exploration tendency can be thought of as the angle Θ(t_c). The value of Θ(t_c) can lie between 0^o and 90^o. An increase in Θ(t_c) denotes higher exploratory tendencies , and hence a larger area of the hypothetical space at t = t_c + 2 years. This resonates with the idea that explorations open up new possibilties. But, reiterating, those new possibilities could be far worse or far better than the ones in original hypothetical space -- the hypothetical space is agnostic to our social values. Theoretical upper limit on Θ(t_c) is 90^o. Beyond that, we would be moving back into the past and defying our only rule.

Beyond this, it starts getting more interesting.
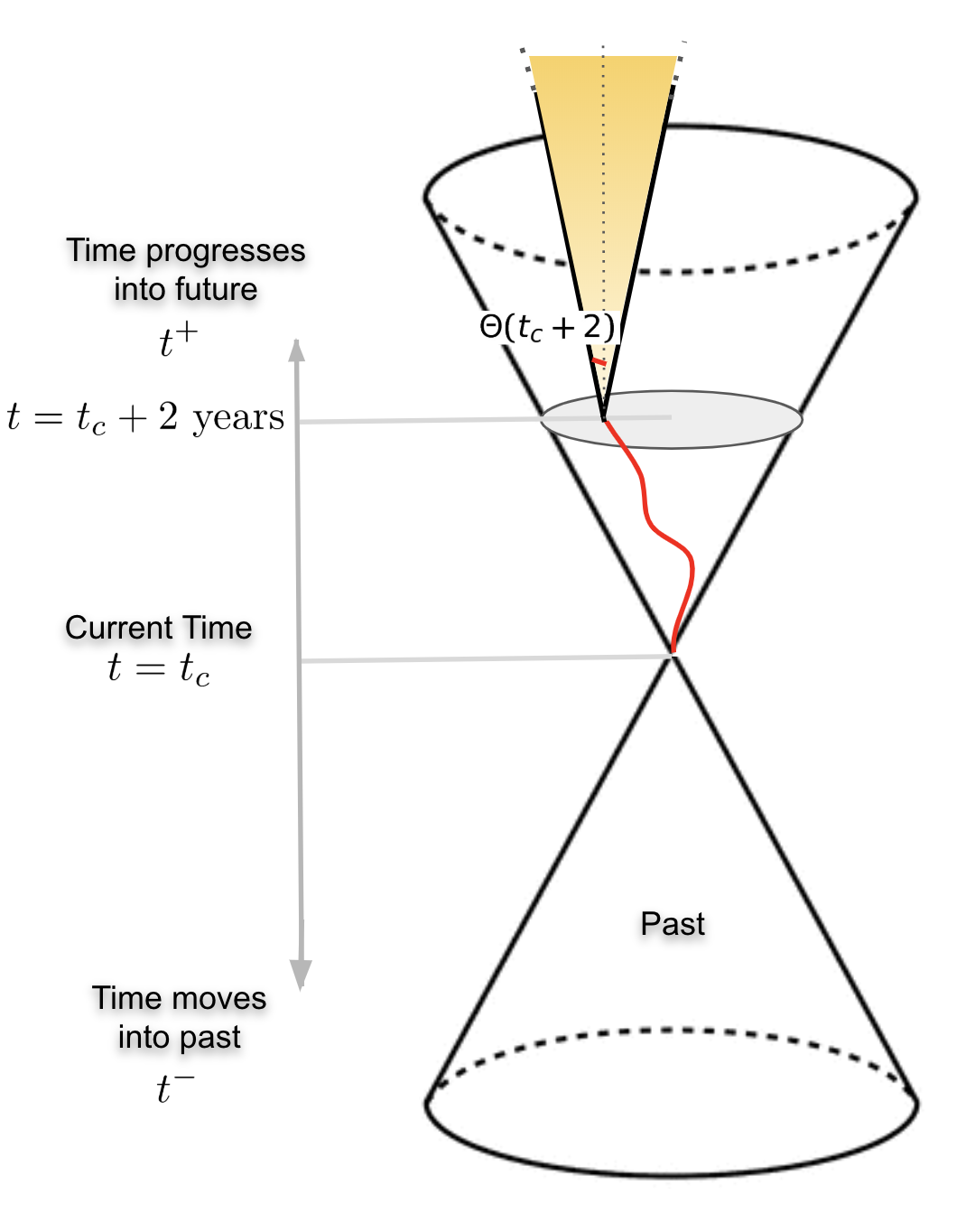
All that we have dicsussed so far, is based on how we perceive the world at t = t_c. As we move into the future, our view of the world changes. Our exploratory tendencies change. Our future cone moves along with us.

By the time we would have reached at t = t_c + 2 years, our future cone would look something like the yellow cone in the figure below. Our tendency to explore would have changed too -- Θ(t_c + 2) instead of Θ(t_c). As it can be noted from the visualization below, in which the exploratory space constricts due to a decreased value of Θ(t_c + 2) compared to Θ(t_c), the hypothetical space at any t > t_c + 2 years will only be a subset of what it would have been when we were at t = t_c. This aligns with the popular idea of having limited options to explore, as we progress into our lives.

However, it is worth noting that this idea of constricting hypothetical space in future is only valid when our exploratory tendencies do not increase considerably with respect to what they were in the past. In other words, at least theoretically, one can always compensate for the loss in future options by increasing their exploratory nature as they progress into future.

The crux of this idea, when ripped off of its visualization and the surrounding mathematics, is similar to how you navigate your way through a pitch-black night with a torch light -- just that you're not allowed to move the torch light. You might possess a torch light with a wider beam (analogous to larger value of Θ(t_c)), which will help you in seeing more from your current standpoint (analogous to t = t_c). Additionally, since you are not allowed to turn around (or walk backwards), if you miss out on a 'potential path' owing to a narrower beam of the torchlight, you may never be able to go where that path could have taken you.

At this point, catering to the strong echoes in my head, here's a link to the poem The Road Not Taken by Robert Frost.

We can make ourselves explore more -- increase Θ(t_c)) -- to open up future possibilities which may be either good or bad (remember that the hypothetical space is agnostic to social constructs).

But exploring is not enough.
We need to move along the red line too.
That 'moving' has to do with the execution. It's easier to move in a straight line than to move in curved lines -- you have to 'move' a lot in a fixed time span. Does it seem analogous to the exploration-versus-exploitation tradeoff in context of multi-armed bandits?

What is the role of "past" cone in visualizing our exploratory tendencies? Does it play a crucial role in visualizing things in retrospect -- what sources could have led you to where you are now at t = t_c? I'll leave these thoughts here for now; may be for another piece in future.

I didn't unconver any secret, but now I have a language and a visualization method to ground my notions of exploratory nature. I hope you do too!